Normalverteilung

Beschreibt eine typische Form von Werteverteilungen, die sich häufig bei um einem zentralen Grenzwert variierenden Zufallszahlen einstellt.

Diese Verteilung kann als eine typischerweise glockenförmige, idealerweise symmetrische, Kurve dargestellt werden und gehört zu den wichtigsten Grundlagen der Stochastik.

Andere Namen

Gaußsche Normalverteilung
[Gaußsche] Glockenkurve

Normal distribution
Gaussian distribution

Beschreibung

Dieser Artikel ist noch in Bearbeitung und daher unvollständig.

Standardabweichung

Die Standardabweichung ist eng mit dem Konzept der Normalverteilung verwandt. Es gilt, dass im Bereich ±𝑠 um den Mittelwert rund 68,3 % der Werte zu finden sind, innerhalb von ±2𝑠 sind es ca. 95,5 %.

Beispiel

Augenzahlenkombinationen beim Würfeln

Ein besonders einleuchtendes Beispiel dafür, wieso sich Zufallsereignissen so oft normalverteilte Wahrscheinlichkeiten auftauchen, findet man beim Würfeln. Wir gehen hierbei von einem normalen, 6-seitigen und fairen Würfel aus, d.h. die Wahrscheinlichkeit für jede Augenzahl, gewürfelt zu werden ist genau gleich.

Bei einem einzelnen Würfel folg daraus, dass es genau sechs Möglichkeiten gibt, jede der möglichen Augenzahlen zu erwürfeln, und jede Augenzahl ist gleich wahrscheinlich, nämlich genau ⅙.

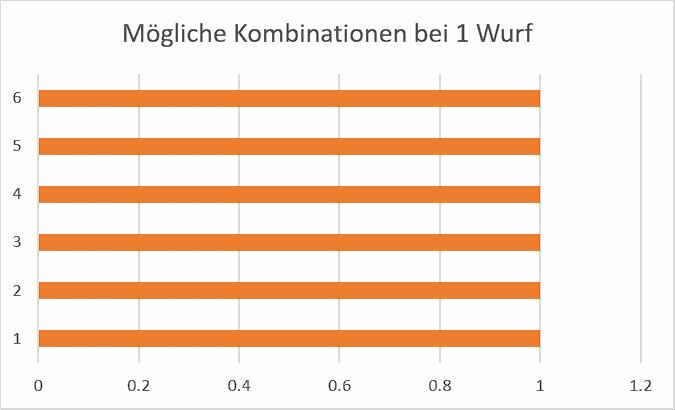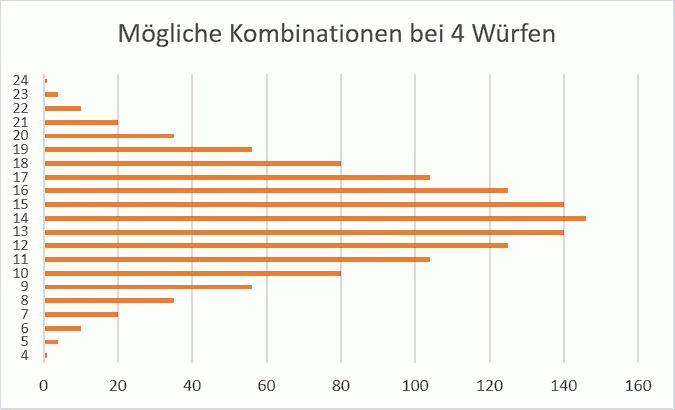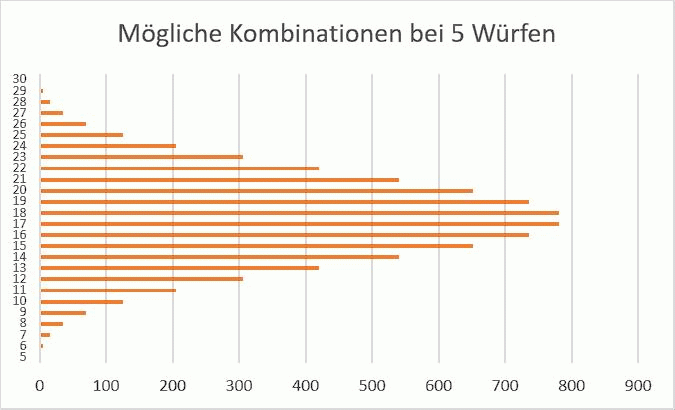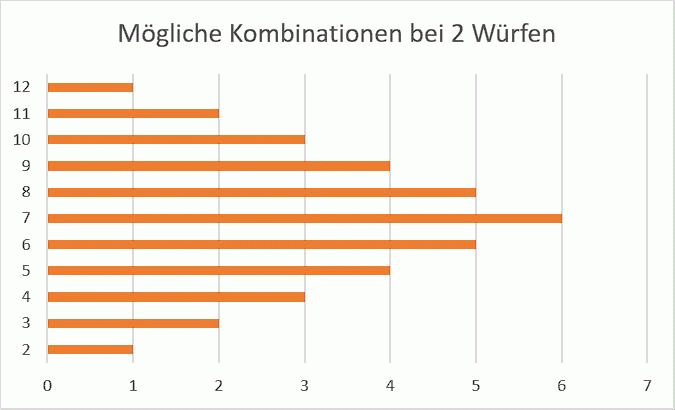
Nimmt man zwei Würfel, wird das etwas interessanter. Es gibt zwar noch immer nur eine Möglichkeit, zwei Augen zu erwürfeln (indem man nämlich zweimal die Eins würfelt), aber bereits für drei Augen gibt es zwei Möglichkeiten: Eins und Zwei sowie Zwei und Eins. Diese Möglichkeit ist damit auch doppelt so wahrscheinlich wie eine Zwei.

Sieben Augen kann man mit zwei Würfeln sogar auf ingesamt sechs verschiedene Weisen erwürfeln: 1+6, 2+5, 3+4, 4+3, 5+2 und 6+1.

Die Animation unten zeigt die möglichen Augenkombinationen für bis zu sechs Würfel. Man kann erkennen, dass sich die Verteilung der möglichen Kombinationen immer mehr an die Normalverteilung annährt, je mehr Würfel benutzt werden.